How exactly is ifcopenshell.geom.create_shape parsing the geometry?
Hello, I want to have the global coordinates of the verts of the IfcBeam object (simple rectangle). The first option was to use:
settings = ifcopenshell.geom.settings()
settings.set(settings.USE_WORLD_COORDS, True)
shape = ifcopenshell.geom.create_shape(settings, element). It works ok, but the geometry is triangulated and I want to have quads (like in my ifc file).
That's why I tried to read the geometry manually from the ifc file using IfcShapeRepresentation Tessellation. To transform the local coordinates to global I used shape.transformation.matrix.data. The thing is the coordinates are not the same and I do not really understand why . (Screenshot #3)
So my questions are: how exactly is ifcopenshell.geom.create_shape parsing the geometry and what am I doing wrong? Thank you very much for your help.
Here are some screenshots to make it clearer:
1). The geometry defined in the ifc file

2). The transformation matrix and the verts from ifcopenshell.geom.create_shape(settings, element)
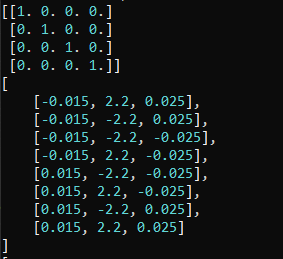
3). Global coordinates from the ifc file (IfcShapeRepresentation Tessellation)



Comments
https://blenderbim.org/docs-python/ifcopenshell-python/geometry_processing.html might help.
https://blenderbim.org/docs-python/ifcopenshell/geometry_settings.html#use-world-coords explains world coordinates. The object placement matrix is multiplied to each coordinate to give global coordinates. In general, I do not recommend you enable this setting unless you absolutely have to.
The faces returned by the shape creation are triangulated, however the edges resemble the original edges (which as you say may be quads, or could be ngons). You'll need to use the edge data if you want to get back your original quads.
@Moult thank you for your answer. I don't understand why the coordinates in the ifc file (Screenshot 1 and 3) are different from the coordinates calculated using ifcopenshell.geom.create_shape (Screenshot 2)? The global and local coordinate systems are the same, so the transformation matrix is an identity matrix. Do you have any idea ? Thank you very much.
Funny when you find a thread trying to do essentially the same thing you want to do.
Could you give any hints on how you do this in code @Moult?
I have a list of edges, faces and verts. I've wrapped my head around the idea of how these lists link with each other. My test cube provides 12 faces (since each quad-side is being interpreted by create_shape as 2 triangles), and provides 12 edges (which are the ones I wish to keep, since these are the 'true' edges which form my quads.
I think I might get there with another coffee, but I am struggling to re-constitute my quad faces from my list of edges... I'm sure once I know, it will make a lot of sense.
@engineer_21 screenshots 1 and 3 are local coordinates. Screenshot 2 is the final global coordinates.
@CSN in https://blenderbim.org/docs-python/ifcopenshell-python/geometry_processing.html the shape.geometry.edges contains the original edges (which may be quads or ngons). With that data, you can "merge triangles".
It's that last bit that I need to think a bit harder to get to. I'll work it out and then report back. Something to do with two faces which only share one edge not included in the edge list... or something.
@CSN here is a Blender implementation https://github.com/IfcOpenShell/IfcOpenShell/blob/v0.7.0/src/blenderbim/blenderbim/tool/geometry.py#L133